Diffie–Hellman Key Exchange
The Diffie–Hellman (DH) key exchange protocol is one of the foundational achievements of modern cryptography. Proposed by Turing Award laureate Whitfield Diffie and Martin Hellman in 1976, it for the first time realized a mechanism for establishing a shared key over an insecure channel, laying the cornerstone for secure communication in the asymmetric encryption system.
Synonyms for Diffie–Hellman key exchange include:
Diffie–Hellman key agreement
Diffie–Hellman key establishment
Exponential key exchange
Diffie–Hellman protocol
While the Diffie–Hellman key exchange itself is an anonymous (unauthenticated) key exchange protocol, it serves as the foundation for many authenticated protocols.
Through exchanging information over a public channel, Diffie–Hellman enables the establishment of a shared secret that can be used for secure communication on the public channel.
The following explains its process (including the mathematical part of the algorithm):
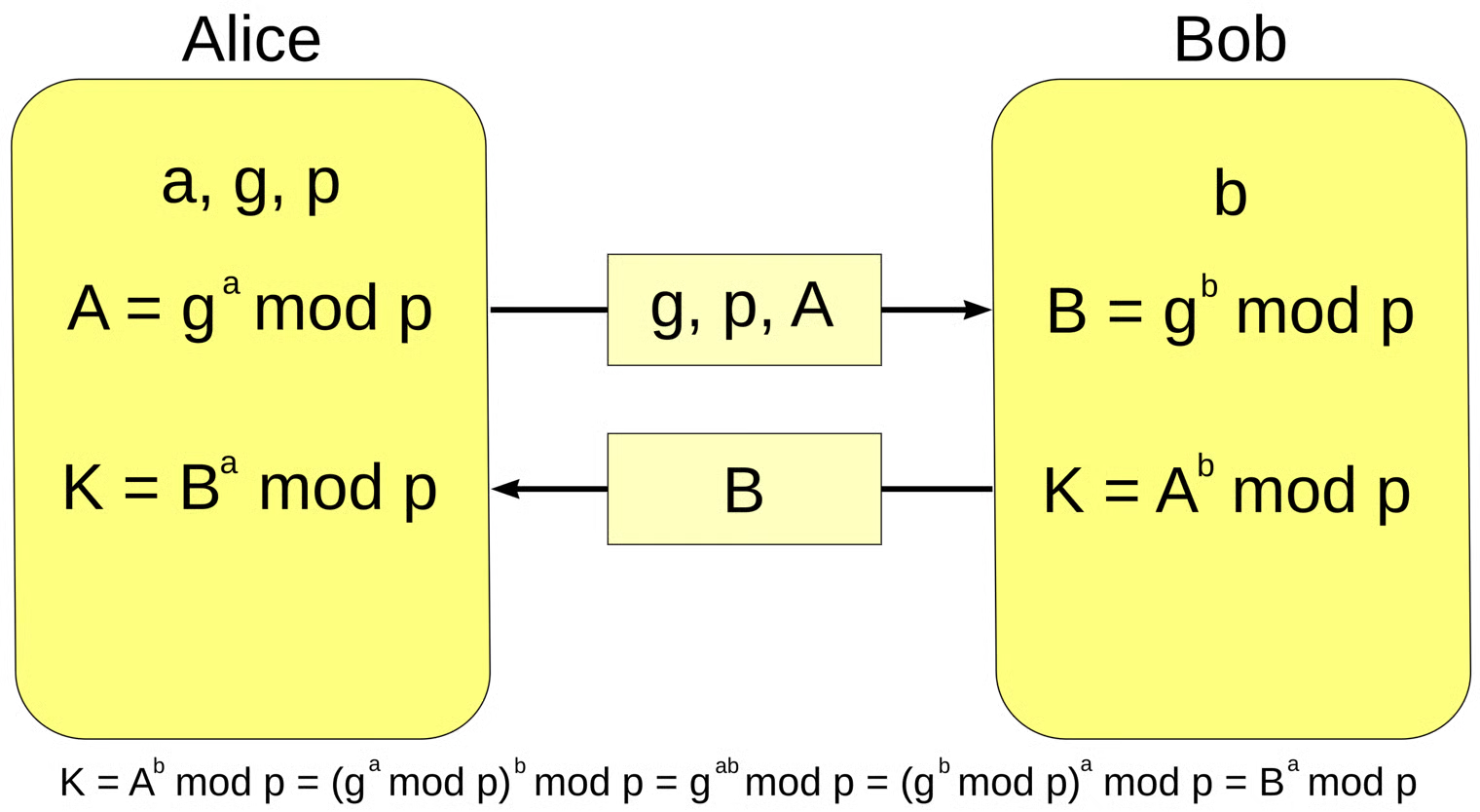
The following diagram helps you understand who knows each piece of information:
(Eve is an eavesdropper — she can see Alice and Bob’s communication content but cannot alter it)
Let s = shared key. s = 2
Let a = Alice’s private key. e.g., a = 6
Let A = Alice’s public key. e.g., A = gᵃ mod p = 8
Let b = Bob’s private key. e.g., b = 15
Let B = Bob’s public key. e.g., B = gᵇ mod p = 19
Let g = public primitive root. e.g., g = 5
Let p = public prime number. e.g., p = 23
Alice： Bob：
p = 23
base g = 5
a = 6
b = 15
A = 56 mod 23 = 8
B = 5b mod 23 = 19
s = 196 mod 23 = 2
s = 8b mod 23 = 2
s = 196 mod 23 = 8b mod 23
s = 2
p = 23
base g = 5
a = 6
b = 15
B = 515 mod 23 = 19
A = 5a mod 23 = 8
s = 815 mod 23 = 2
s = 19a mod 23 = 2
s = 815 mod 23 = 19a mod 23
s = 2
Eve （eavesdropper）：
p = 23
base g = 5
a = 6
b = 15
A = 5a mod 23 = 8
B = 5b mod 23 = 19
s = 19a mod 23
s = 8b mod 23
s = 19a mod 23 = 8b mod 23
s = 2
Security
When appropriate G and g are selected, this protocol is considered eavesdrop-secure. An eavesdropper like Eve would have to solve the Diffie–Hellman problem to obtain gab, which is currently regarded as a computationally hard problem. If an efficient algorithm for solving the discrete logarithm problem is developed, it could be used to simplify the calculation of a or b, thereby solving the Diffie–Hellman problem and rendering many public-key cryptosystems (including this one) insecure.
The order of G should be a prime number, or it should have a sufficiently large prime factor to prevent the use of the Pohlig–Hellman algorithm to derive a or b. For this reason, a Sophie Germain prime q can be used to compute the prime p=2q+1；
such a p is called a safe prime because the order of G can only be divisible by 2 and q when p is used. Sometimes, g is chosen as a generator of the q-order subgroup of G rather than G itself, so that the Legendre symbol of ga does not reveal the lower bits of a.
If the random number generators used by Alice and Bob are not fully random and are predictable to some extent, Eve's task will be much simpler.
Ephemeral DH (D-H Ephemeral, DHE) can provide forward secrecy.
Authentication
In its original description, the Diffie–Hellman key exchange itself does not provide identity authentication for both communicating parties, making it vulnerable to man-in-the-middle attacks. A man-in-the-middle can perform two separate Diffie–Hellman key exchanges in the middle of the channel—one with Alice and another with Bob—successfully impersonating Bob to Alice and vice versa. The attacker can then decrypt (read and store) messages from either party, re-encrypt them, and forward them to the other. Therefore, a mechanism to verify the identities of both communicating parties is usually required to prevent such attacks.
There are many secure authentication solutions that utilize the Diffie–Hellman key exchange. When Alice and Bob share a public key infrastructure (PKI), they can sign their returned keys or sign ga and gb (as in the MQV protocol); STS and the IKE component of the IPsec protocol have become part of Internet protocols; when Alice and Bob share a password, they can also use password-authenticated key agreement based on the Diffie–Hellman algorithm, similar to ITU-T Recommendation X.1035. This has been adopted as the home network standard for G.hn.
Application in the DF Protocol
n the DF Protocol, we adopt the elliptic curve variant ECDH (Elliptic Curve Diffie–Hellman) as the core algorithm of the communication encryption layer. The end-to-end shared key between nodes is established through the following steps:
Each node generates a pair of elliptic curve private and public keys (using curves such as Curve25519 or secp256r1);
Nodes exchange public keys, while private keys are stored locally and not disclosed;
Both parties independently compute a consistent shared key using the other party's public key and their own private key;
The shared key is used to derive a symmetric key (e.g., AES-256 session key) to encrypt subsequent data transmission.
Since the computational security of ECDH is based on the Elliptic Curve Discrete Logarithm Problem (ECDLP), it is difficult to crack even with modern computing resources. In addition, the DF Protocol further enhances long-term security against man-in-the-middle attacks and quantum computing threats by frequently updating session keys, introducing Perfect Forward Secrecy, and providing optional lattice-based cryptography auxiliary channels.This mechanism ensures that both ends of the communication can establish a symmetric key without relying on third-party trust, realizing an end-to-end secure link and forming the encryption foundation of the DF Protocol's trusted communication system.
Last updated